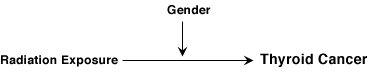
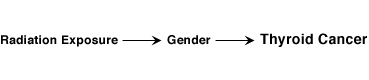
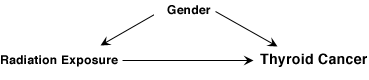
A cohort study was conducted to examine the relationship between radiation exposure and thyroid cancer. The researchers were concerned that gender was a potential confounding variable.
How would you evaluate this hypothesis? Keep in mind the properties of a confounder...
- A confounder must be a risk factor for the outcome
- A confounder must be associated with the exposure under study
- A confounder cannot be in the causal pathway of interest
Step 1: What diagram is consistent with the hypothesis?
Step 2: Is gender a risk factor for the disease under study?
| TC+ | TC- | |
| Female | 256 | 543 |
| Male | 64 | 736 |
RR =
Step 3: Is gender associated with the exposure under study?
| Radiation + | Radiation - | |
| Female | 319 | 480 |
| Male | 480 | 320 |
RR =
Step 4: Is the gender in the pathway of interest? (Does radiation exposure lead to gender, which in turn, leads to thyroid cancer?)
Now, with the three 'confounder criteria' fulfilled, you can test if gender confounds the exposure-disease relationship...
Step 5: Calculate the "crude" estimate.
The crude estimate (in this case the risk ratio, or RR) is the basic association between your exposure and outcome of interest.
What is the crude RR of the radiation exposure-thyroid cancer relationship?
| TC+ | TC- | |
| Radiation + | 180 | 619 |
| Radiation - | 140 | 660 |
RR =
Step 6: Examine the exposure-disease relationship after stratifying on your proposed confounder.
What do we mean by stratification?
We have hypothesized that gender is a confounder of the radiation exposure-thyroid cancer relationship. Gender has two levels (female and male). You want to see if there is a relationship between the exposure and disease within each stratum of the proposed confounder (i.e., Is there an association between the exposure and disease among females only? Is there an association between the exposure and disease among males only?)
Step 7: Once you have stratified your data, you need to calculate the risk ratio in each stratum of the potential confounding variable.
| All Females | ||
|---|---|---|
| TC+ | TC- | |
| Radiation + | 134 | 185 |
| Radiation - | 122 | 358 |
RR =
| All Males | ||
|---|---|---|
| TC+ | TC- | |
| Radiation + | 46 | 434 |
| Radiation - | 18 | 302 |
RR =
Step 8: If the stratum-specific estimates are not significantly different from one another, you can use a statistical test to pool your stratum-specific estimates across strata (i.e., Mantel-Haenszel procedure).
Here, the pooled risk ratio (the average of the stratum-specific estimates calculated above) is 1.7.
Step 9: The rule of thumb in evaluating confounding is to look at the percent change in the adjusted estimate. If the adjusted estimate differs from the crude by 10% or more, then it is customary to consider that variable a confounder.
Does the adjusted estimate (RR=1.7) differ from the crude estimate (RR=1.3) by 10% or more?
Step 10: Does gender confound the radiation-thyroid cancer relationship?
- Yes. Gender fulfills the 3 properties of a confounder and upon stratification, we find that the adjusted estimate is differs from the crude by more than 10%.
- No. Gender fulfills the 3 properties of a confounder but upon stratification, the adjusted estimate does not differ from the crude by more than 10%.
- Gender does not fulfill the 3 properties of a confounder.
Great job! That is the end of the questions.