Our ability to reject the null hypothesis depends upon several related concepts:

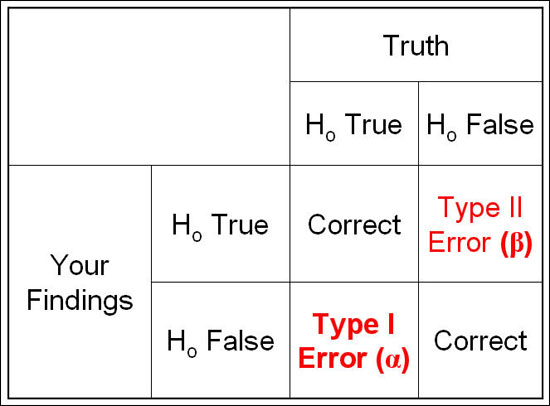
Alpha (a): Conventionally set to be 0.05, although this is somewhat arbitrary. This represents probability of committing a Type I error, which is the probability of rejecting the null hypothesis given that that the null hypothesis is true. In other words, we conclude that there is a relationship between E-D, when the observed association is actually due to chance.

Power (1-β): Where β (type II error) is defined as the probability of failing to reject the null hypothesis when it is in fact false. In other words, we conclude that there is no relationship between E-D when, in fact, it exists. The probability of correctly rejecting the null hypothesis is equal to 1-β , which is called power. The power of a test refers to its ability to detect what it is looking for.

Type I & Type II Error:

Sample size: A larger sample size leads to more accurate parameter estimates, which leads to greater precision and higher power to correctly find true associations between exposure and disease. However, a larger sample size increases the expense and difficulty of the study. A graph can be a useful way of making the best decision regarding the trade-off between power and sample size. Notice that the rate of increase in power starts to reduce dramatically at around the 80% power figure. An appropriate sample size can then be determined, based on expense and desired power.

Effect Size: The magnitude of the association we are trying to estimate in our population. Large effects are easier to detect than small effects. One question that is often encountered in power analyses is, how much of an effect are we interested in, or what is a 'clinically relevant' effect, or what effect size should we expect to see? The guiding principle in estimating an 'a priori' effect size is to base it on the best available prior knowledge. What has previous research found? We can set the magnitude of the measure of association we are trying to estimate based on the literature describing Susser Syndrome. In general, the smaller the effect size we want to detect, the larger our study size needs to be for a given power value.